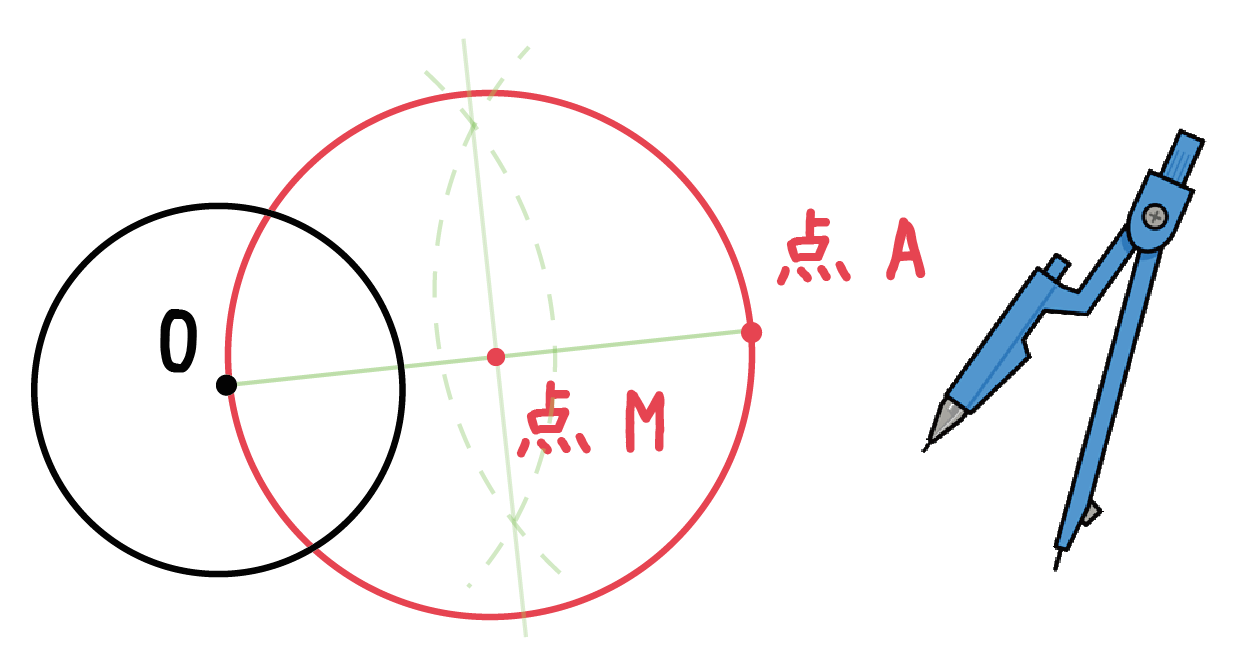
VBA Tips Excel19 with Windows10 2点を通り半径Rの円の中心を求める 2点と半径から中心を求める計算式としては、「2つの円の方程式をもとに連立方程式を解くとよい」とネットで説明があったが、連立方程式はイマイチ面白くなかったので、他の方法が無いか自分で図を書いて求めてみました。円の中心の求め方 ある2点(円周上のどこかであることに限定 円の方程式の求め方まとめ!パターン別に解説するよ! 数スタ;すなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
円の中心点の求め方 コンパス
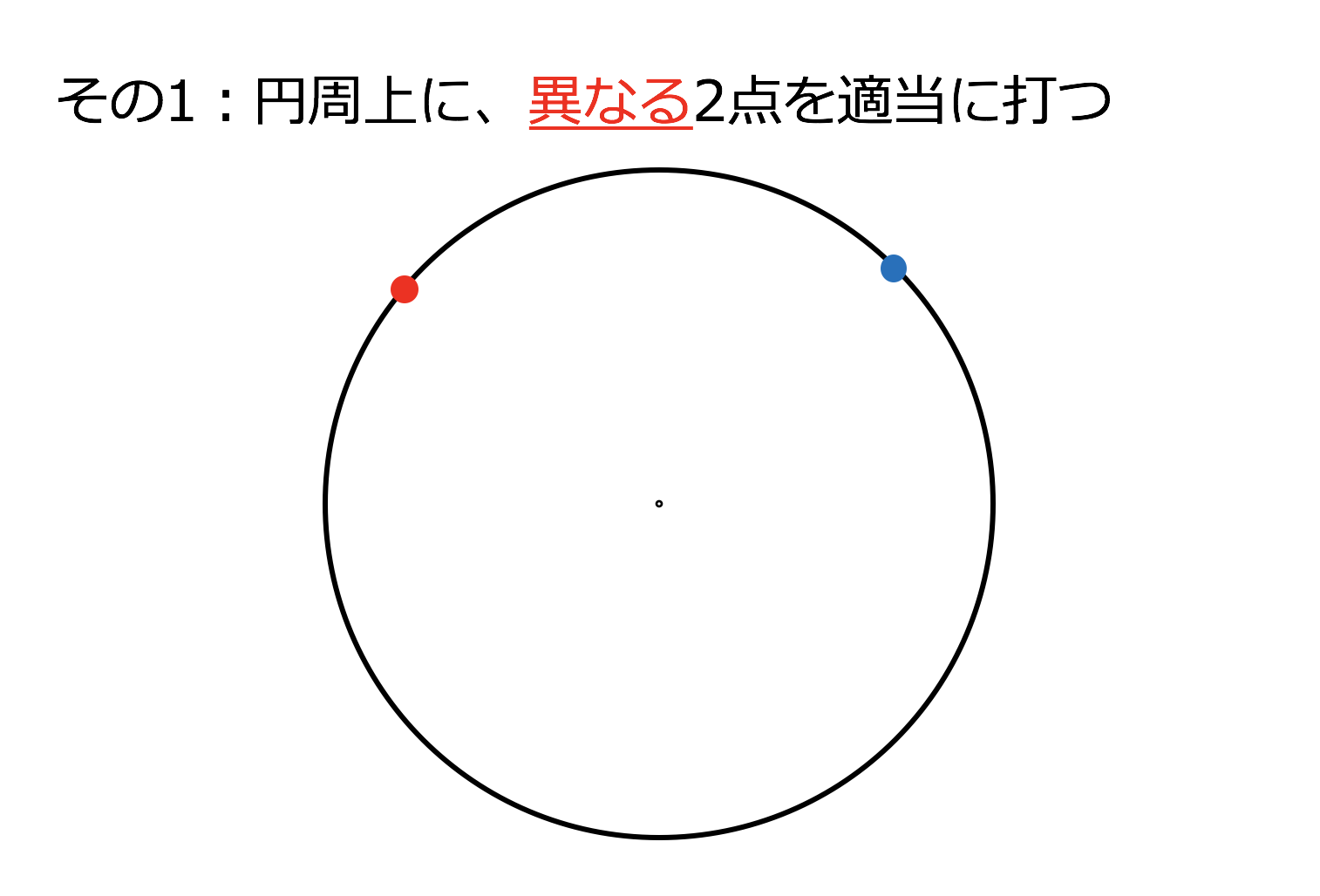
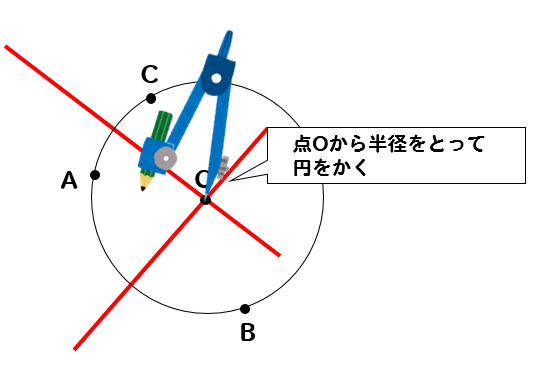
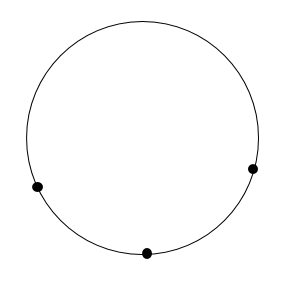
円の中心点の求め方 コンパス-円周上の点はどこでも,円の中心から等距離であるという性質を利用します。円周上に適当な3つの点を決め,その3点から等距離にある点を作図から求めます。 ここで紹介している内容は17年3月時点の情報です。ご紹介している内容・名称等は変わることがあります。 ※ このq&aでは、 「進研左ツールバーの『 点 』タブをクリックします。 円の上で 右クリック して、そのまま3時方向にドラッグします。 クロックメニューが現れたら、マウスボタンを放すと中心点が表示されます。



中1 作図 円の中心を求める方法を解説 数スタ
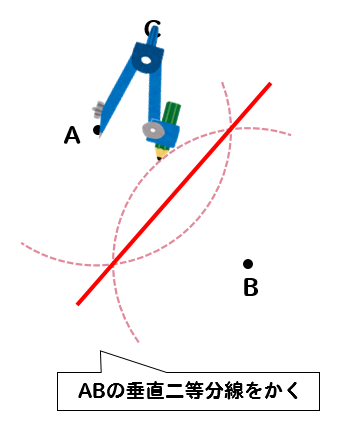
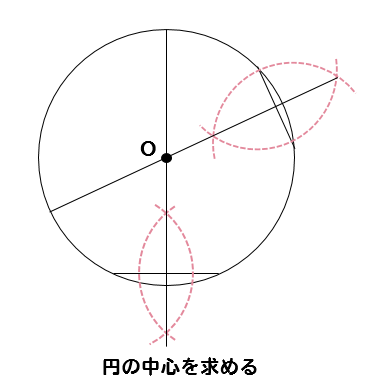
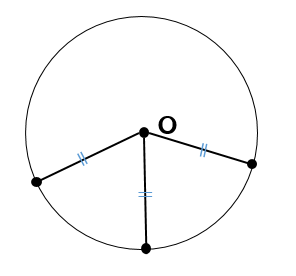
空き缶の中心の見つけ方 1、空き缶の円を紙に写し取ります。 直角の物(ハガキなど)を置きます。 (Pの位置) 3、直角の物と円が交わる2点に印を付けます。 (AとB) 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 (Oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり!中心の座標が (x 0, y 0) 半径 r の円 (x − x 0) 2 (y − y 0) 2 = r 2 と、直線 a x b y c = 0 の交点を求める。 上記求め方の考え方により、まずベクトル C H →, H A → を求める必要がある。3点を通る円の中心と半径を求める 点 A (x 1, y 1) 、点 B (x 2, y 2) 、点 C (x 3, y 3) を通る円の中心 P と半径 r を求める。
円の方程式は の他に ① と表すこともできます。 ※円の中心、半径の長さがわかる時に使用 ※3つの点を通ることがわかっている時に使用 このようにして使い分けます。 それでは早速、①を使った問題をみてみましょう。 3点(2,1)、(4,-7)、(-1,-3)を通る円の方程式を求めよ ①式にそれぞれ代入をして指定した3点を通る円の式 困っていたのでありがたいです。 計算過程も書いてあると尚嬉しいです。 タンクの中心からずれた位置へ差し込むパイプの長さを求めました。 半径rと x座標a,c,e から y座標b,d,f が求められればサイコーです! アンケートにご点の位置が決まったら、円の中心から点の位置までの距離を求めます。距離はx二乗 y二乗で求められます。 仮にxとyの値が両方とも05ならば025 025 = 05となります。 12行目のif文では円の中に収まっているかどうかの判定を行っています。点の位置であるx
円の中心点を簡単に出す使い方 円の中心点を求めることも図面作成中によくあることだと思います。 円の中心点を出すのは、以外と難しいものでそう簡単には出すことができません。 しかし、 Jw_cad なら数クリックで簡単に出すことができる機能が備わっています。 今回はその機能を使って簡単に円の中心点を出す使い方の練習です。 簡単なアニメを作ってみた円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45°MixiExcel(エクセル)活用 円の半径を算出したいのですが 円形状の物体をXY軸上で一定の間隔でトレースし、円の半径(直径)を求めることを検討しています。 測定機器はレーザーを照射し、一定の間隔に物体があればその物体との距離(高さ)の値を拾ってきます。



中1 作図 円の中心を求める方法を解説 数スタ




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径Xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135°直角に回転したパスの交わるところが円の中心になっているはずです。 本当でしょうか? 選択ツールで円を選択します。 きちんと円の中心と直線パスの交差しているところが円の中心だとわかりますね。 さてここからが本題です。




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト



中1 作図 円の中心を求める方法を解説 数スタ
外接円の方程式の求め方 例題1:3点O(0,0),A(12,6),B(6,8)を頂点とする三角形OABの外接円の方程式を求めよ このように垂直二等分線がどれも明らかでないときはaのやり方で解くことになります。 答え 外接円の中心を(a,b),半径をRとすると次が成り立つ。 a 2 b 2 =R 2 (a12) 2 (b6) 2 =R 2 (a6) 2 (b8) 2 =R(該当円の中心点から、母点が存在しない方向に引いた線がボロノイ辺となります。) ※ドロネー図は母点を頂点として、三角形で分割したものです。 3母点の接点円の中心の求め方 母点p1、p2及びp2、p3の垂直2等分線をy1=a1x1+c1 y2=a2x2+c2とする それぞれ2点u, vを固定したとき, この2点を通る円の中で 包含円となりうるものは何通りあるか? u v 赤側 青側 u, v以外の点を直線uv に 関して2分割 赤側と青側 各点について,その点と u, vを通る円を求めたとき, 青側の点は,青側に中心 をもつ半径最大の円の 内部




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア



円周角と中心角 中学から数学だいすき
より,円の方程式は (x − 3) 2 (y − 2) 2 = 2 (x3)^2(y2)^2=2 (x − 3) 2 (y − 2) 2 = 2 となります。右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B)3点を通る円 円は一直線上ではない3点の座標があれば一意に決定します。 下図を参照してください。ここで、3点の座標を、 (x1, y1), (x2, y2), (x3, y3) 求める中心座標を、 (Cx, Cy) 求める半径を、 r とします。
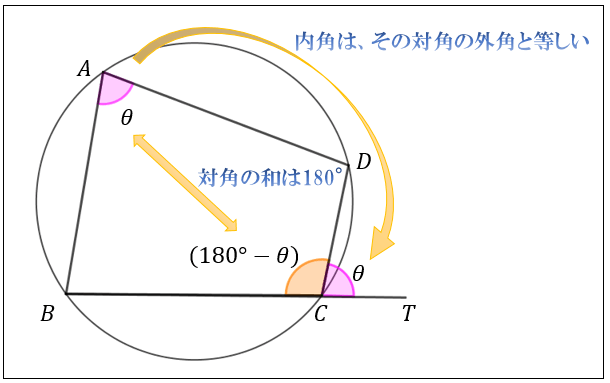



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



作図 円に内接する正三角形の作図方法とは 数スタ
中点の座標の求め方 ①与えられた直線に垂直で中心を通る 直線をつくる。 ②①で作った直線と与えられた直線の 交点が弦の中点の座標となる。 円の接線の方程式に関する取り扱い 原点中心・円上の点があたえられたとき x y r円 2 2 2 上の点 a b, における接線の方程式は ax by r 2 原点中心・円外曲率について 二階微分可能な曲線 y = f (a) y=f(a) y = f (a) は (a, f (a)) (a,f(a)) (a, f (a)) 付近で円に近似することができます。 その円を曲率円,半径を 曲率半径 と言います。 曲率半径が大きいほどカーブはゆるいです。 曲率 は曲率半径の逆数です。 曲線の(局所的な)曲がり具合を表しま円の中心と半径を求めれば円の方程式が計算できます。 円の中心は2点の中点なので (3, 2) (3,2) (3, 2) 半径は2点間の距離公式より 1 2 1 2 = 2 \sqrt{1^21^2}=\sqrt{2} 1 2 1 2 = 2 ;




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
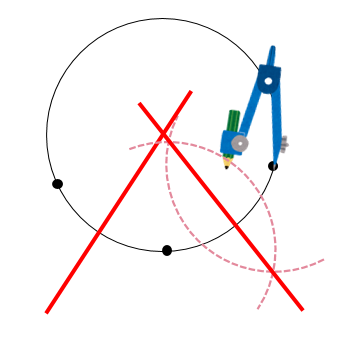



中1 作図 円の中心を求める方法を解説 数スタ
次に、円の方程式の求め方について解説していきます。 問題のパターンによって、基本形・一般形の使い分けます。 中心の座標と半径が与えられている場合 中心の座標と半径が与えられている問題では、円の方程式の基本形を使います。 円の方程式(基本形) 円の中心が点 \(\mathrm{A}(a, b同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90°BC:円曲線始点(Beginning Curve) EC:円曲線終点(End Curve) IP :交点(Intersection Point) R :半径(Radius of curve) I :交角(Intersection Angle) O :中心点 BP:路線始点(Beginning Point) EP:路線終点(End Curve Point) TL:接線長(Tangent Length) CL:曲線
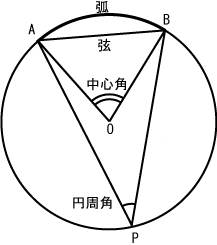



円 数学 Wikipedia




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
多角形の中心点の座標の求め方 数学 6 図形の重心を取るプログラムを教えてください その他(教育・科学・学問) 7 台形の重心を求めるには その他(ビジネス・キャリア) 8 Excelを使用して円弧の半径を最小二乗法で求めたい Excel(エクセル) 9 円の中心座標ってもとめられます中心が原点で、半径2の円ということから \(a=0, b=0, r=2\)を当てはめていくと $$x^2y^2=4$$ となります。 中心\((2, 3)\)で、半径5の円ということから \(a=2, b=3, r=5\)を当てはめていくと $$(x2)^2(y3)^2=25$$ となります。Step2:円の中心座標$(a,b)$を求める 上で求めた直線$l_{ij}$の方程式に$(i,j)=(1,2),(2,3)$を代入して2直線$l_{12}$, $l_{23}$の方程式を作ります.2式を連立して$x,y$について解けば,円の中心座標$(a,b)$を求めることができます. Step3:円の半径$r$を求める
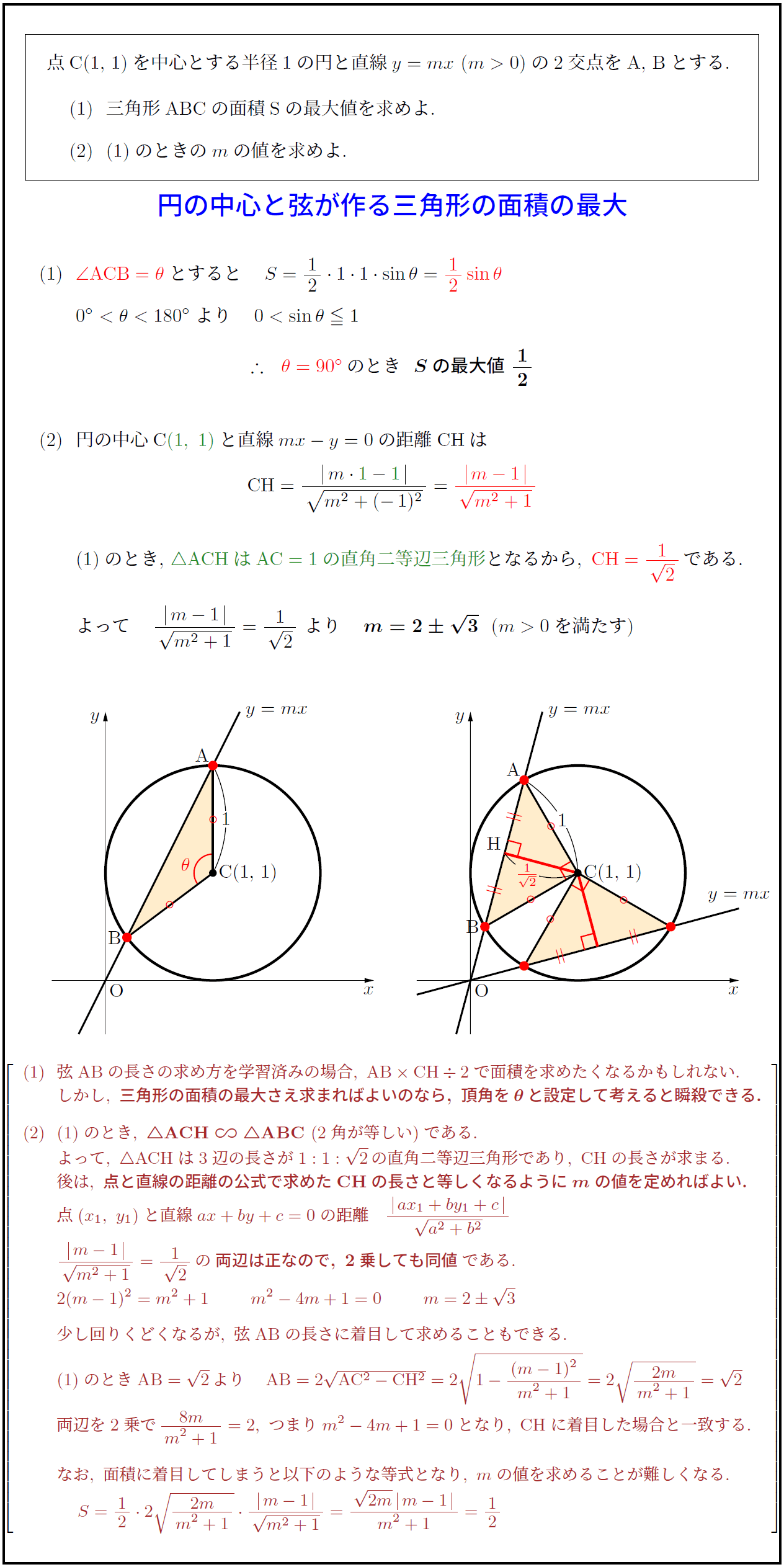



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月
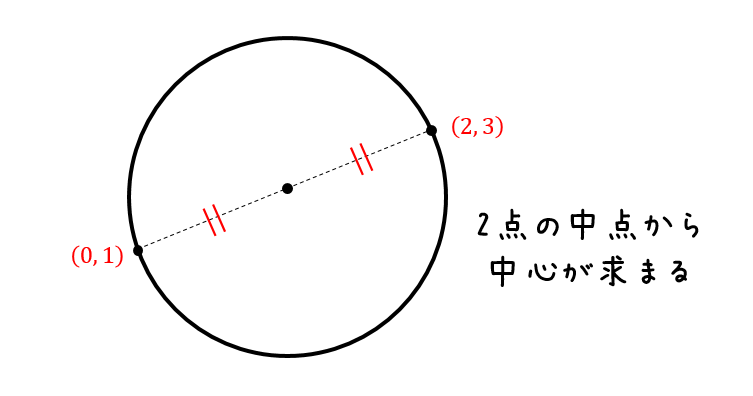



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
半径 r の円Cの中心Aと直線lの距離を d とします。 ポイントの図のように、 中心と直線との距離が半径より小さい とき、2点で交わりますね! よって、 d<r⇔「異なる2点で交わる」 「d=r」ならば「1



円の中心の求め方 Love金沢水彩画




三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
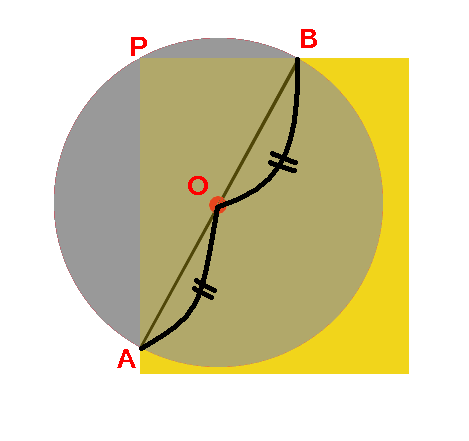



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




中1 作図 円の中心を求める方法を解説 数スタ




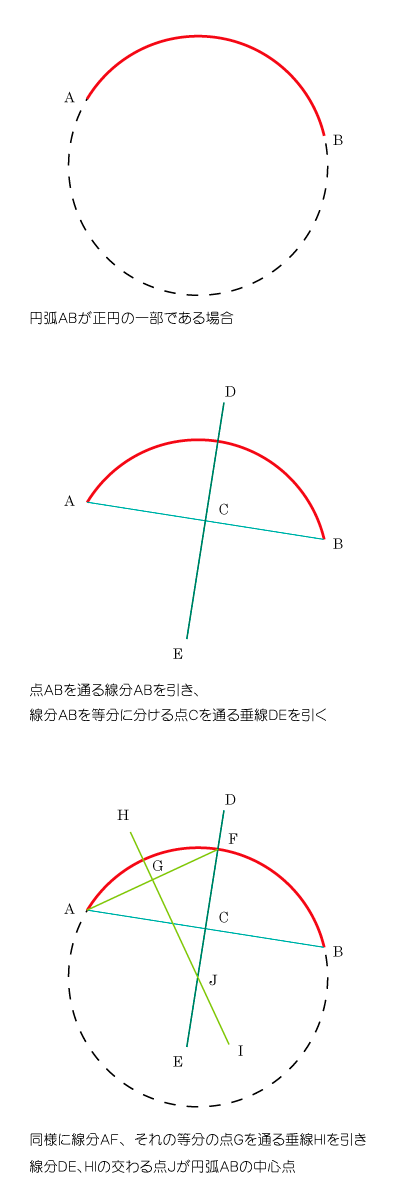
数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



1



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




円の中心の出し方 コンパスなし 直径わからない編 シャンハイ山本弾工房



3次元空間での円の中心の求め方 Inak Engineering Llc




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート




中1 作図 円の中心を求める方法を解説 数スタ



Studydoctor円の公式と なぜ 中学1年数学 Studydoctor



1




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート
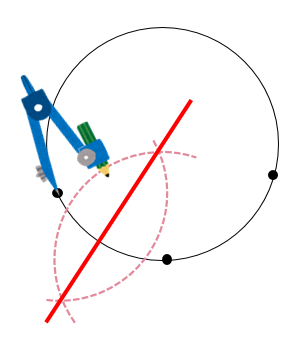



中1 作図 円の中心を求める方法を解説 数スタ




この問題の の中点の座標の求め方を教えて下さい 至急です Clear



1
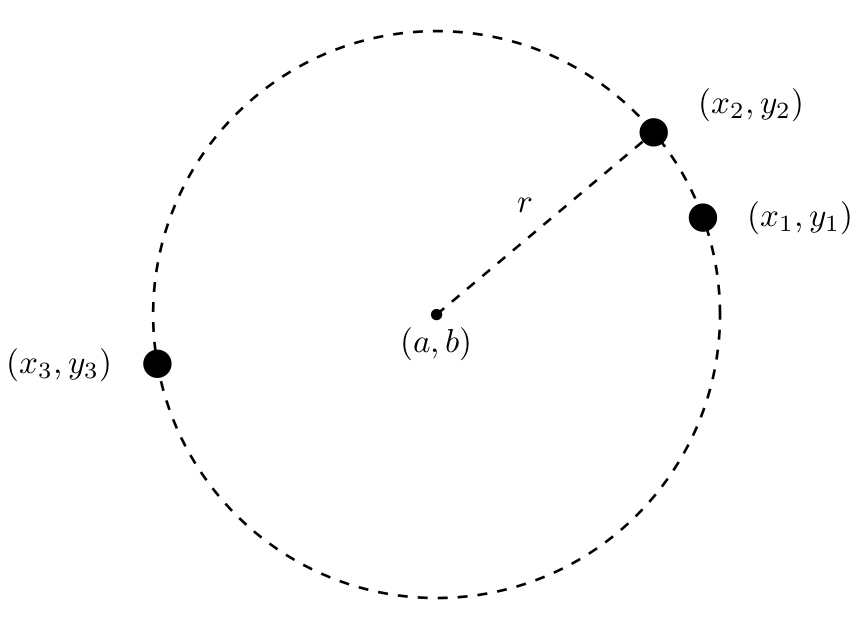



3点を通る円の中心と半径 Notes Jp




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



コンパスと定規を使った渦巻き線 アルキメデスの螺旋 の描き方 図形の描き方022a 夏貸文庫



円の中心を求める方法を教えてください 条件 小学生にも理解 Yahoo 知恵袋



基本の作図




円の中心を求める 3つの方法 Wikihow




円の中心を求める 3つの方法 Wikihow




円の中心を求める 3つの方法 Wikihow




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



幾何計算 2点と半径から円の中心点を求めます Satoh
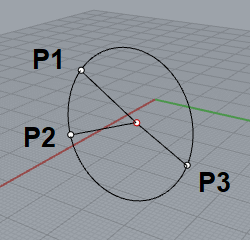



3次元空間での円の中心の求め方 Inak Engineering Llc




円の中心を求める 3つの方法 Wikihow




Aの求め方を教えてください 点oは円の中心です 答えは174 です Clear



1




基本 円の方程式 なかけんの数学ノート




最後の2円の中心間の距離の求め方が分かりません Clear
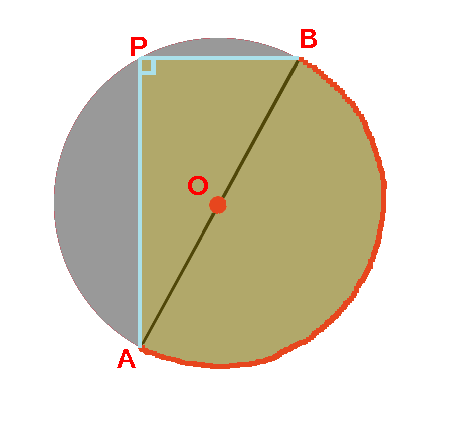



空き缶の中心の見つけ方 綿菓子を自宅で作ろう



こんにちは 円の中心を通らない場合どうやって解いたらよいかわかりま Yahoo 知恵袋



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




Aの求め方を教えてください 点oは円の中心です 答えは174 です Clear




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア



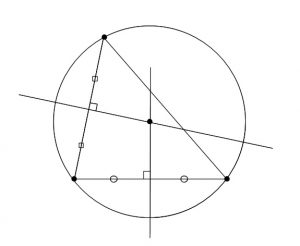
中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




図のような点oが中心の円においてxの角の求め方 画像を添付しますこ 数学 教えて Goo




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



サイト インペリアル はげ 円の中心の求め方 コンパスなし Tenpo Syukyaku Jp
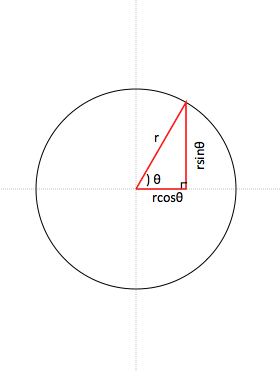



円の中心からの角度から真円の円周上の座標を計算する Gamesprit



イメージ図のような直線と1点を通る接円の中心座標もしくは半径の求め方の式を教 Yahoo 知恵袋
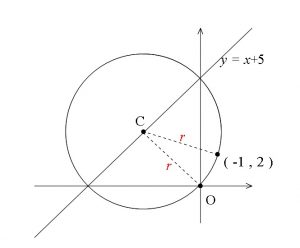



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary



二次元図形における円周上の座標 X Y を求める方法を教えてくだ Yahoo 知恵袋




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
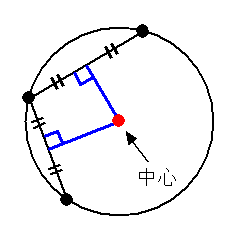



3次元空間での円の中心の求め方 Inak Engineering Llc



From灘 円の中心の求め方 朝日小学生新聞 中学受験eye 関西圏



幾何計算 2点と半径から円の中心点を求めます Satoh




円の中心を求める 3つの方法 Wikihow



幾何計算 2点と半径から円の中心点を求めます Satoh




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
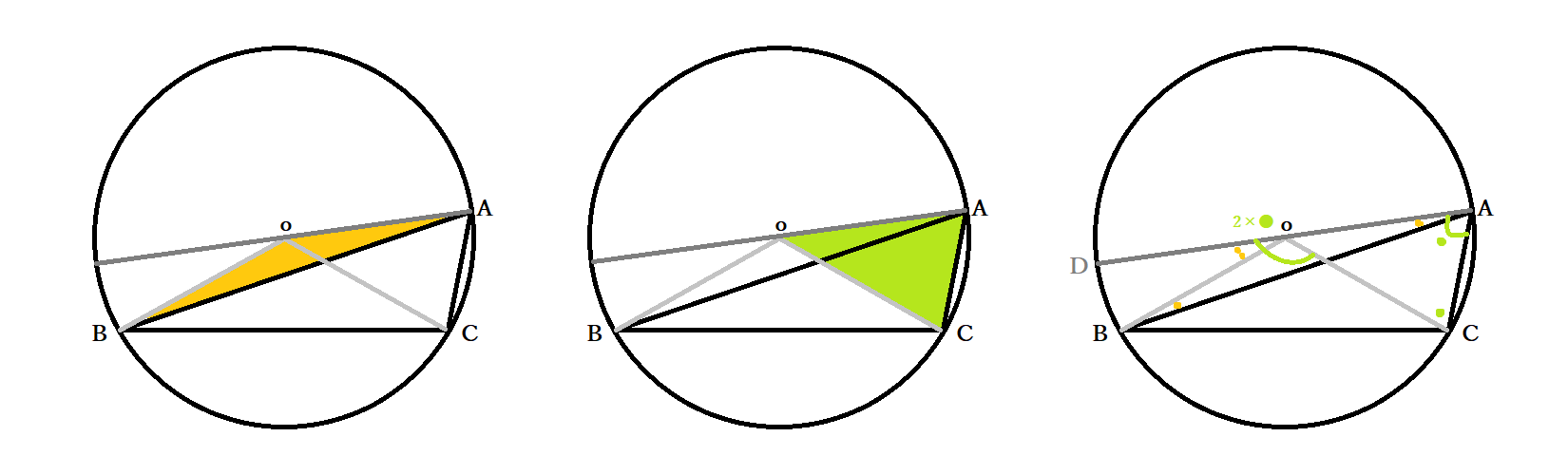



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary




作図 05 円の中心の求め方 Youtube
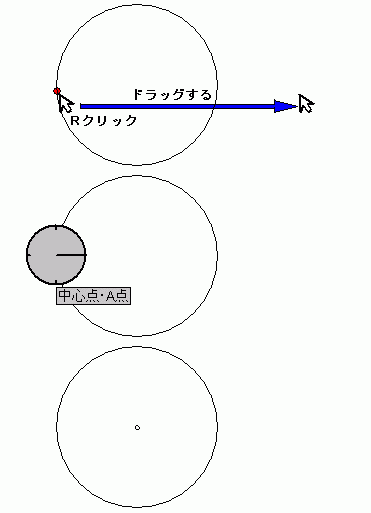



円の中心点




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



幾何計算 2点と半径から円の中心点を求めます Satoh




中心点の求め方をお願いします Cadでの製図の問題の解き方をお願い Cad Dtp 教えて Goo




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
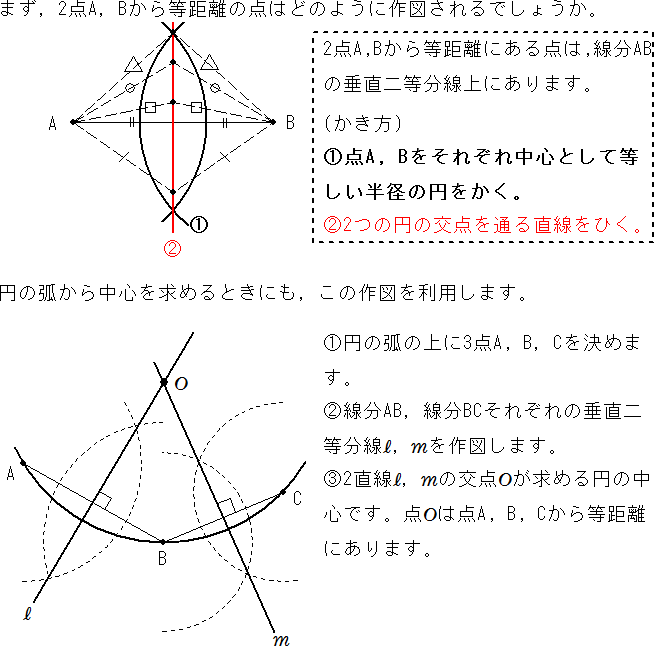



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト
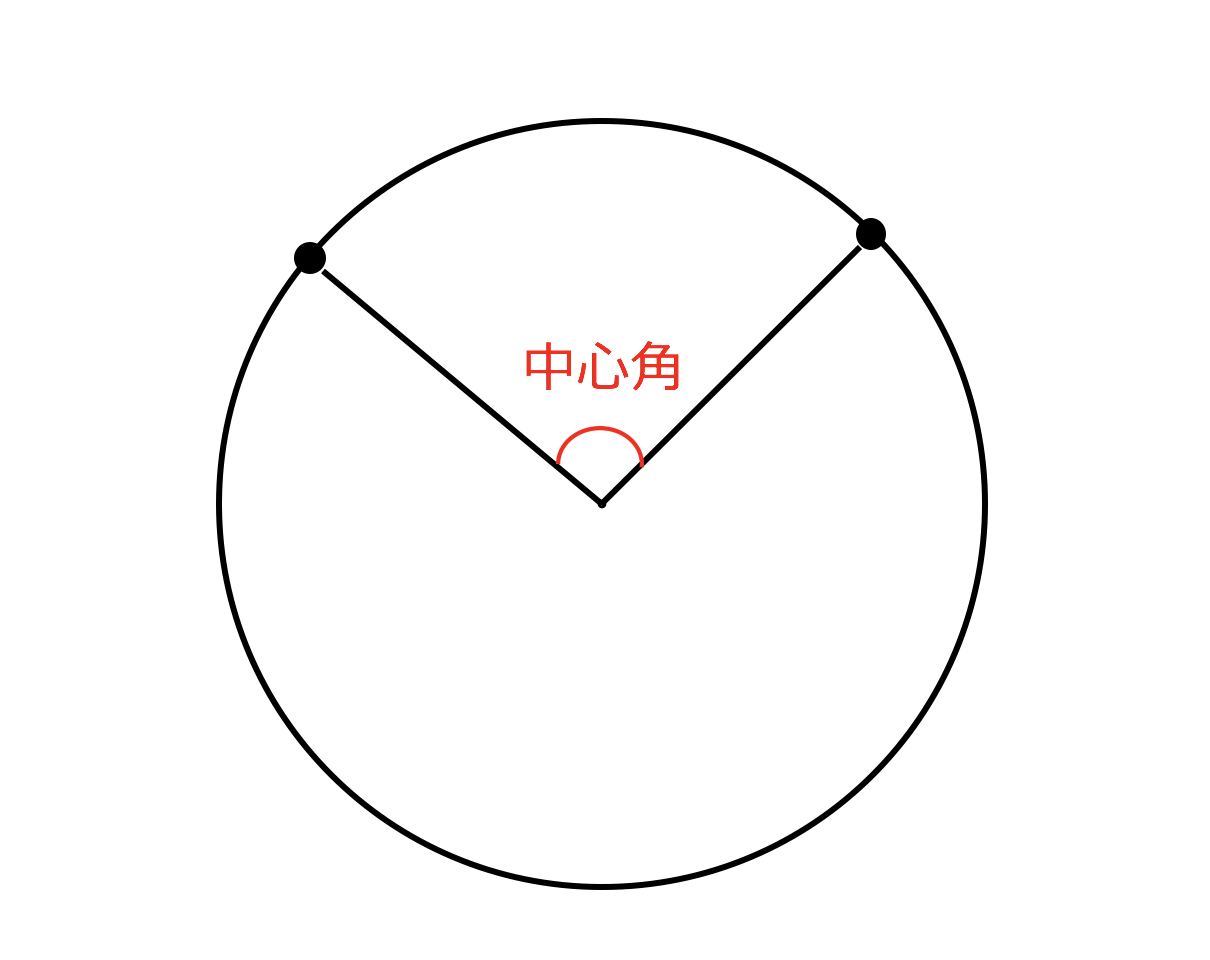



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室



点oは円の中心です Xの求め方がわかりません 解き方を教えてください Yahoo 知恵袋



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




円の方程式と関連問題 座標 ベクトル 複素数 高校数学の美しい物語




円の中心を求める 3つの方法 Wikihow




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト
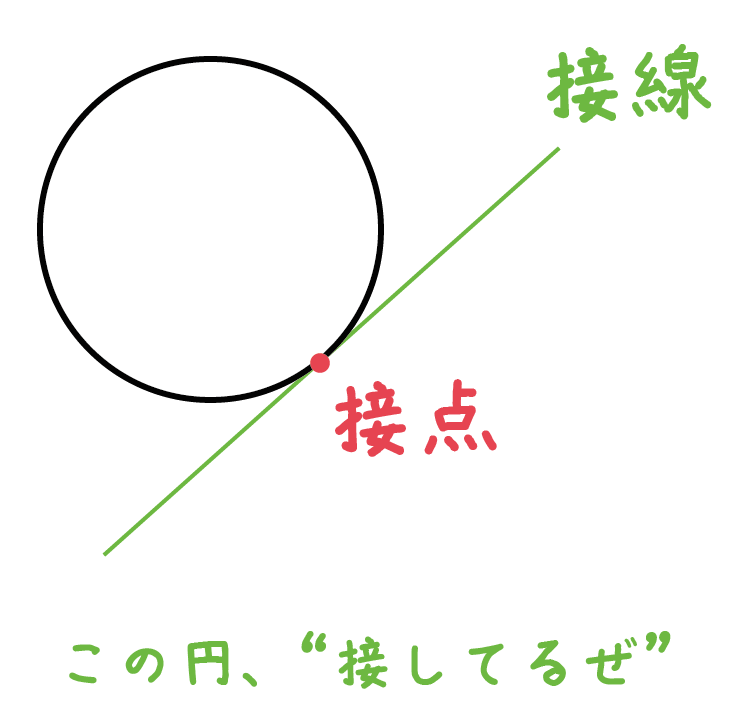



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



中1 作図 円の中心を求める方法を解説 数スタ




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
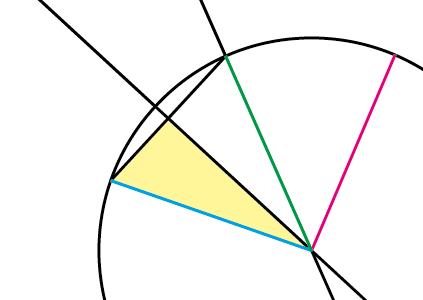



数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




円の中心を求める 3つの方法 Wikihow



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典
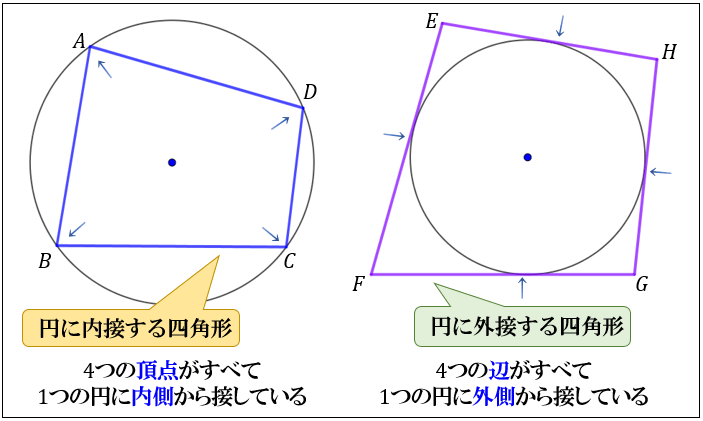



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
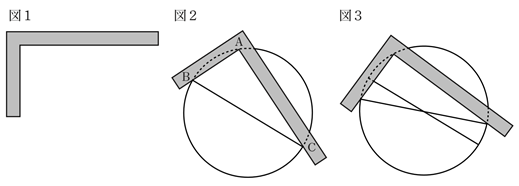



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級
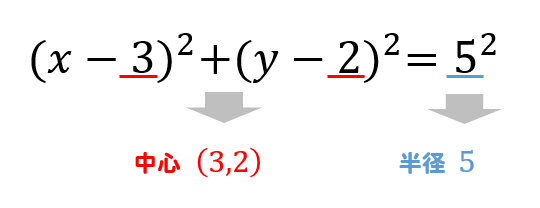



円の方程式 中心の座標と半径の求め方を解説 数スタ




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用


