「11 – ポリゴン1 – 一辺の長さを指定して多角形を描く」へ最初のコメントを投稿しませんか? vip会員ならコメントを投稿できます! vip会員について詳しく知る ログインしてコメントを書く一辺の長さが a の正 n 角形の、任意の点から m 番目に近い点までの距離は、 a sin m π n sin π n {\displaystyle {a\sin {m\pi \over {n}} \over {\sin {\pi \over {n}}}}} である。 今回は、正方形の対角線の長さを計算してみます。 もちろん、中学3年生の数学で習う内容なので、「計算方法など考えなくても、覚えてしまえばいいじゃないか」と思う方もいるでしょうが、それを小学校で習う知識で工夫して求めるのが、中学受験・適性検査には求められます。 例題 一辺
八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋
正八角形 一辺の長さ 求め方
正八角形 一辺の長さ 求め方- 正多角形の面積を求めます。 高校数学の問題集に載ってるレベルの問題です。正 角形の1辺の長さを 、重心(正 角形の外心と一致する) o と頂点の距離を (これは外接円の半径でもある)とします: 図中の点 a, b は正 角形の隣り合う頂点、点 m は辺 ab の中点です。ひし形の面積は?1分でわかる求め方、公式、辺の長さ、対角線との関係 正方形の対角線は?1分でわかる値、公式、長さの計算、辺の長さとの関係 平行四辺形とは?1分でわかる意味、定義、角度、面積、長方形と正方形との関係 管理人おすすめ!




続 円周率の話 正八角形を 更に正12角形を使って円周率パイを計算 一滴tka
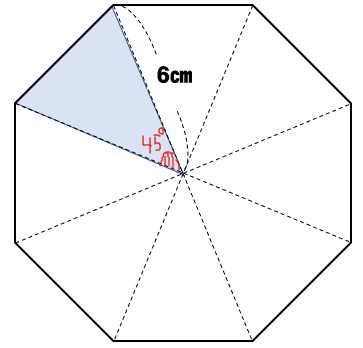
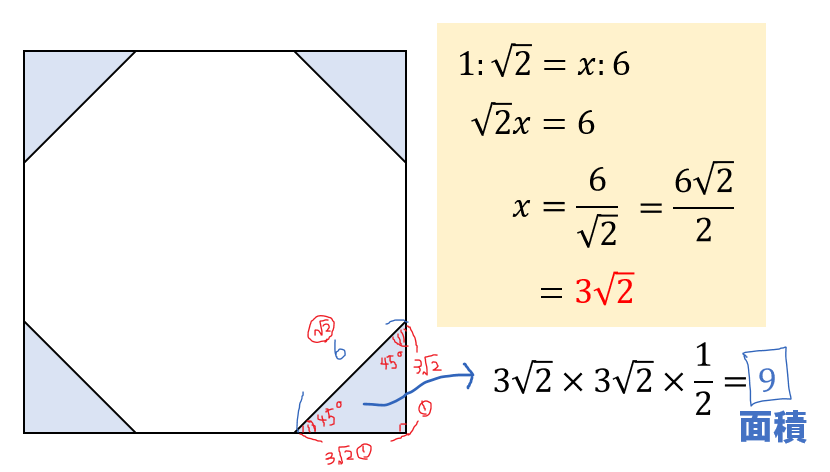
外角は図2のような角では ない 各内角には2つの外角があるが,外角の大きさというときにはそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° にここでは、半径1の円に内接する正五角形の一辺の長さを計算して、正五角形の作図方法を説明します。 正五角形の内角は 2π/5 2 π / 5 ラジアン(72°)であることから、 まず最初に a=cos(2π/5) a = cos ( 2 π / 5) を使って一辺の長さを計算します。 右の図に従っ三平方の定理4 解説 1辺6cmの正八角形の面積を求めよ。 図のように補助線をひき、各点に記号をつける。 正八角形の一つの内角は 135°なので ∠HAK=90°、∠BAK=45°また、∠AKB=90°である。 すると AKBが直角二等辺三角形になるので AB=6cm, AK=BK=3 2 cmとなる。 CLD, FME, HNG も同様になる。 それら直角二等辺三角形の面積は 3 2 ×3 2 ÷2=9
教育現場の先生方に役立つ、授業のヒント。 教育現場で使えるアイディアが盛りだくさんのカシオ計算機の教育情報サイト。 関数電卓 例題と操作 辺の長さが わかる 正三角形の 面積を √を 残したまま(1)で求めた$35$個の三角形のうち、正7角形と2辺を共有するものは、 abcと合同な三角形 の1種類しかできない。(図A) この三角形は、正7角形の隣り合う辺を共有する。言いかえれば、正七角形のひとつの頂点の両側の辺を共有する。Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。
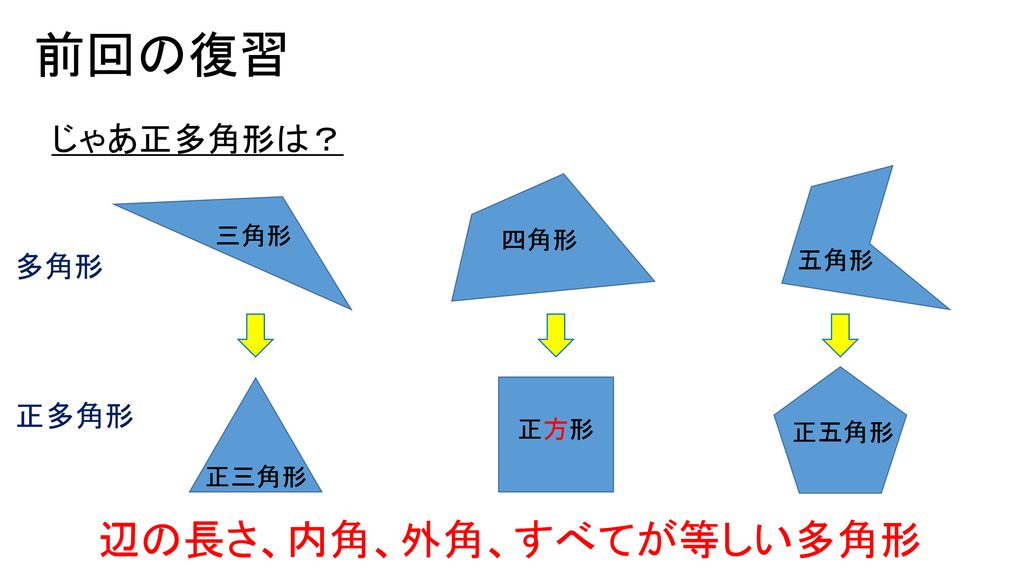
13年06月19日 (水) 三角関数使って表記すれば半径1の円に内接する正N角形の一辺の長さは 2sin(π / N) なんですが、この値は具体的に加減乗除と累乗根を使って表すことができます。 それを計算してみようという試み。正八角形 正八角形 においては、一つの 外角 と 中心角 は 45 ° で、 内角 は135°になる。 一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。 A = 2 a 2 cot π 8 = 2 ( 1 2 ) a 2 ≈ 4843 a 2 {\displaystyle A=2a^ {2}\cot {\frac {\pi } {8}}=2 (1 {\sqrt {2}})a^ {2}\approx 4843a^ {2}} cos ( 2 π / 8 ) {\displaystyle \cos (2\pi /8)} を有理数と平方根で表すことが可能である。点 正多角形と円 1① ₁ にあてはまる言葉を書きましょう。 ( 点) がすべて等しく,角の大きさも



5年算数 円と正多角形 1 わかる教え方



半径1の円に内接する正n角形の一辺の長さ 元祖ワシ的日記
θ = 180 (1 − 2 n)一辺の長さだけでなく他の情報(角度など)が分かれば面積を求めることができます。 例題3 一辺の長さが $2$ で、一つの角度が $60^{\circ}$ であるひし形の面積を求めよ。 解答正八面体とそれに内接する内接球の図です。 表面積は簡単に計算できて、一辺の 長さが1の正三角形が八面あるので、(ルート3/4)X8です。 表面積: 2ルート3 (図1、 Functionview で作成) 上図において、辺ADと辺BCの中点をそれぞれ 点G と 点H とします。 点E、点F、点 Gと点Hを含む平面で正八面体をカットしたときの断面図を図2に示します。 四角形




数学ia 組合せに関する問題の考え方 三角形の個数 大学入試数学の考え方と解法



一辺の長さ1である正八角形の面積の求め方わかる人教えてください 外 Yahoo 知恵袋
r 2 ×12=12r 2 =3×4r 2 =3× (2r) 2 = 3R2な正三角形である。 辺CD上に30㎝(03m)おきに花を7つならべると, 辺CDの長さは, となり,18mになる。正三角形は3つの辺の長さが等しいので, 円の半径にあたる辺ACも18mになる。 円周は,直径×円周率で求められるから,この円の円周は,正5角形の1辺の長さと対角線の長さの比が黄金比であることから,定規とコンパスを使って正5角形を作図することができます.長さが の線分は,直角をはさむ辺の長さがそれぞれ 1/2 と 1 である直角三角形の斜辺として作図することができます.これを 1/2 だけ延ばすと,黄金比が作図できた
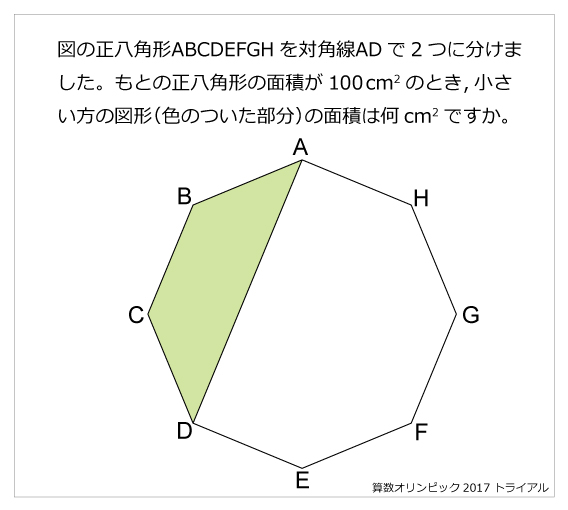



算数オリンピック 17年 トライアル 算数星人のweb問題集 中学受験算数の問題に挑戦




1辺の長さが4cmの正八角形の面積を求めよ という問題があるのです Okwave
正三角形 ・正三角形(辺から高さと面積) 正三角形の1辺の長さから高さと面積を計算します。 ・正三角形(高さから辺と面積) 正三角形の高さから1辺の長さと面積を計算します。 さて、実際に正四面体の体積を求めます。 ここでは、先ほど説明した 正四面体の高さ を用います。 一辺 の正四面体の体積 一辺 の正三角形の面積 底面積 高さ となります。 正三角形の面積について復習したい方はこちらも参照してください。 3分で 《1辺の長さの求め方》 1辺の長さ×4=まわりの長さ であることから 1辺の長さ×4=30 答え 75cm 問題⑤ 面積が54㎠のひし形の対角線の1つが6cmのとき、もう1つの対角線の長さは何㎝でしょう? 《対角線の長さの求め方》
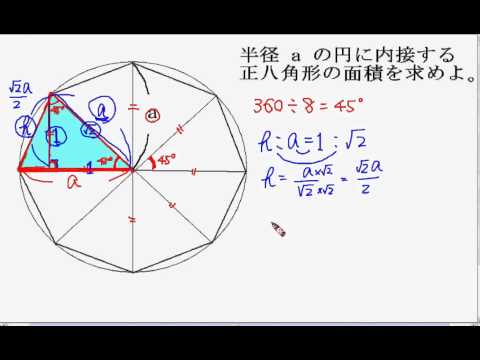



中3数学 正八角形の面積 Youtube



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
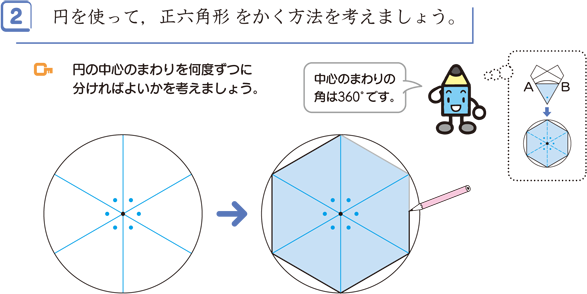
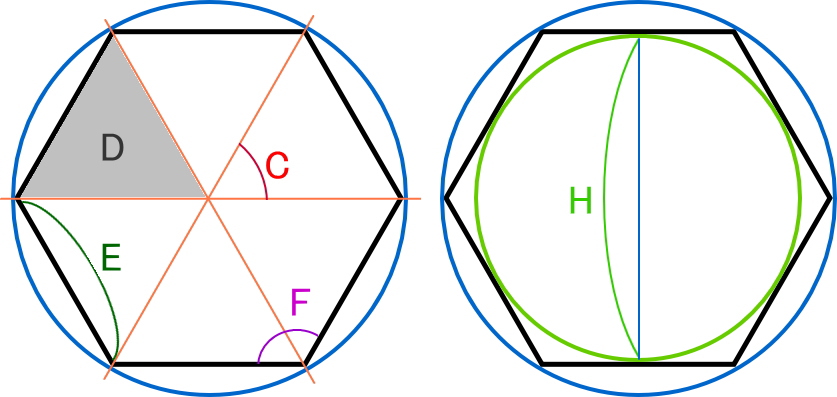
ま円をもとにつくった八角形は,二等辺三角形OABが8つでできているから,8つの辺の長さと角の 大きさが等しい。 ~辺の長さがすべて等しく,角の大きさもすべて等しい多角形を「正多角形」といい,正八角形という ~ 関正多角形の性質を,辺の長さ 一辺が長さ1の正五角形がある。 対角線を5本引くと、その内部に小さな正五角形ができます。 元の正五角形と内部にできる正五角形の面積の比を求めよ。 同じく正17角形の場合はどうなるか? 3時間考えても回答にいたりませんでした。正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の
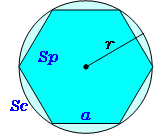



円に内接する正多角形 高精度計算サイト



正多角形の内接円の半径 倭算数理研究所
まずは正十角形の外角1つ分の大きさを求めます。 $$360 \div 10=36°$$ 内角は\(180(外角)\)より $$=144°$$ となります。 内角の和を考えて求める場合には $$180 \times (102)=1440°$$ 内角の和をこのように求めて 10で割ってやれば求めることができます。 $$1440Length= qrt(Area /(2 2 * qrt(2))) 2の平方根を取り、結果に2を掛けて2を加え一辺6cmの正八角形の面積を求めよ。 図のように補助線をひき、各点に記号をつけます。 正八角形の一つの内角は135 なので ∠HAK=90 、∠BAK=45 です。 よって AKBが直角二等辺三角形なので AB=6cm, AK=BK=3 2cm となり 正八角形面積求め方, 正八面体の表面積・体積




Plumbago 雑記 数学 八角形の周の長さから見る円周率 円周率 余弦定理
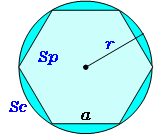



正多角形の外接円 高精度計算サイト




小5 算数 小5 54 正多角形 Youtube



八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋
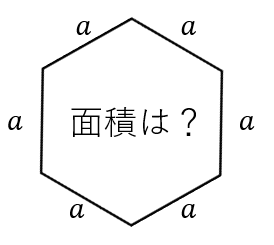



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学



正多角形と円周の長さ プロアンズ



コンピュータプログラミング演習 Cpii 中間テスト 最終 06 01 27 実施 06 02 03 返却 制限時間90分 点満点 Http Www Tuat Ac Jp Kamelab Cpii 05 0603 Answer0603 Html 解答及び採点基準 第1問 以下は 半径r 100 0 の円に内接する正n



正六角形角度 平面図形の角度 Lousi Imagine



八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋




正多角形の対角線の長さ 香料ゐっすゐの夢



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ
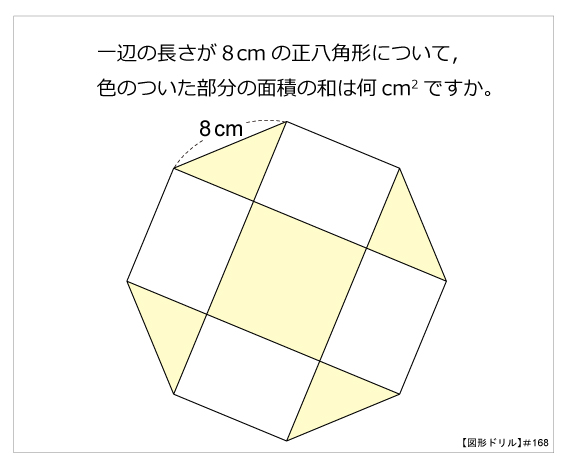



図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



8角形の面積



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫



正多角形 算数用語集




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月




辺の長さの異なる六角形の面積 辺の長さの異なる六角形の面積 向き合 数学 教えて Goo



3




八角形 Wikipedia



正 角形 正多角形 を表にしてみる エクセル関数の使い方
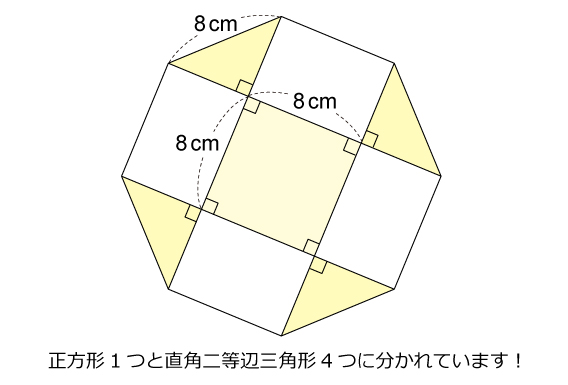



図形ドリル 第168問 正八角形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい 答えでは余弦 Yahoo 知恵袋



一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい 答えでは余弦 Yahoo 知恵袋



東大入試問題 円周率が3 05より大きいことを証明せよ



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫
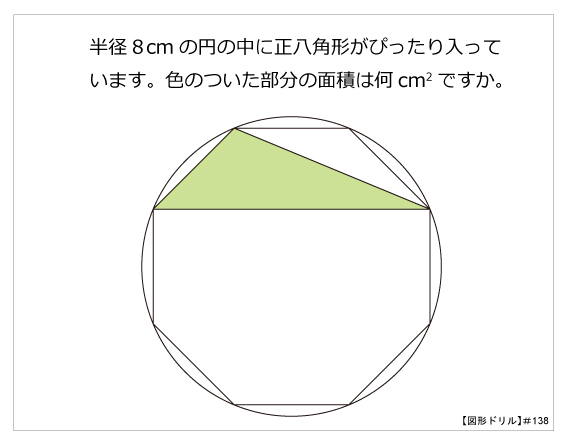



図形ドリル 第138問 正八角形と半径 算数星人のweb問題集 中学受験算数の問題に挑戦




続 円周率の話 正八角形を 更に正12角形を使って円周率パイを計算 一滴tka




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information
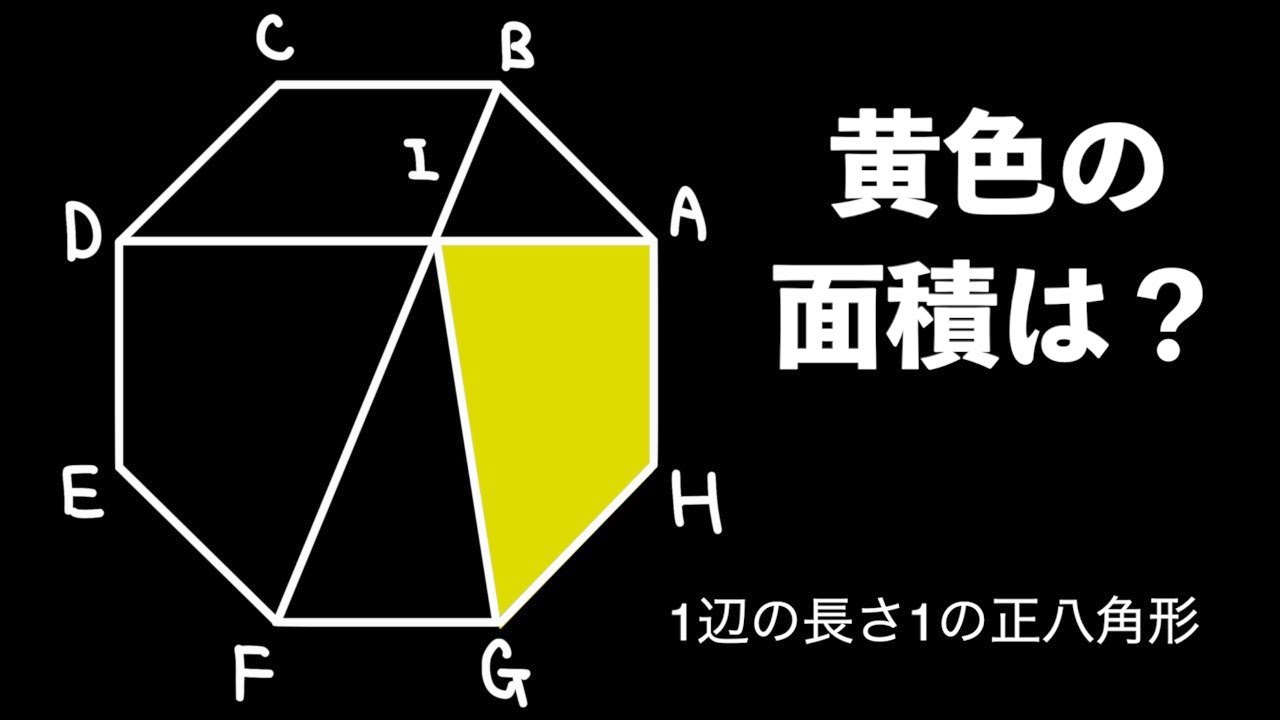



正八角形の領域面積 Youtube




中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




角形の対角線の本数問題 18年 横浜市立南高等学校附属中学校 恋する中高一貫校 適性検査 徹底攻略



一辺1の正八角形の対角線の長さを教えてください Aeの長さの出し方を教えてく Yahoo 知恵袋




5年生算数 正多角形と円 円周の長さと直径の長さの関係を調べよう Youtube



一辺2cmの正八角形の面積を教えてください 図があまり上手くあ Yahoo 知恵袋




八角形鏡加工について アンティークミラー Com




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information



半径aの円に内接する正八角形の面積の答えを計算式とともにお願 Yahoo 知恵袋
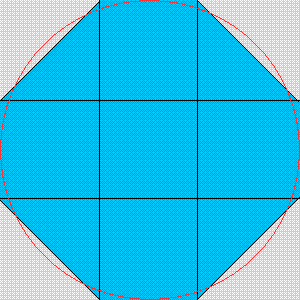



Pont157 円周率の近似値を求めるやけに簡単な方法




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




数学 図形 中3です 塾のテキストに載っていた問題です 下の図の正 Okwave



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




正八角形の作図 正方形から正八角形の作図の仕方を教えてください 数学 教えて Goo
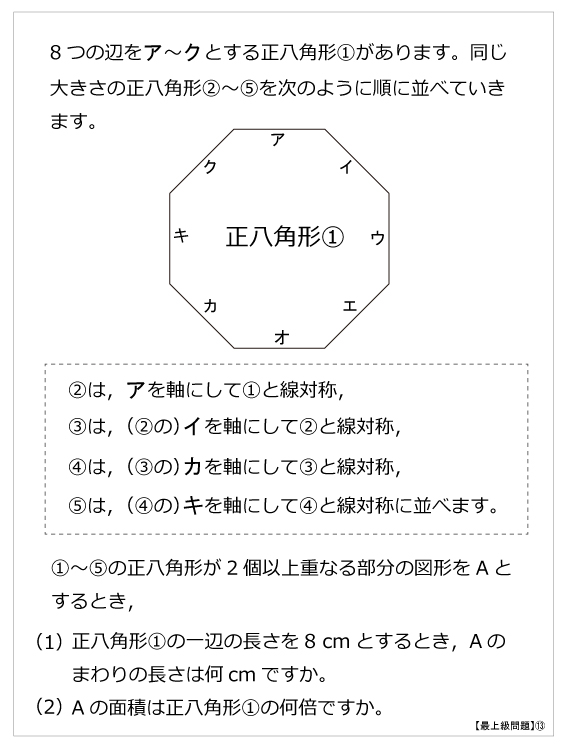



最上級問題 正八角形の問題 算数星人のweb問題集 中学受験算数の問題に挑戦




5年算数 円と正多角形 1 わかる教え方



八角形のお盆




ベリースライム Berryslime3 Twitter
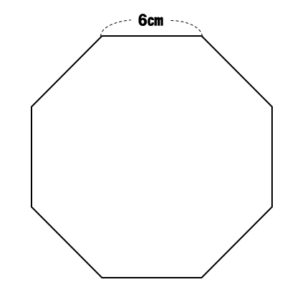



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい 答えでは余弦 Yahoo 知恵袋




八角形の周囲と面積を計算する方法
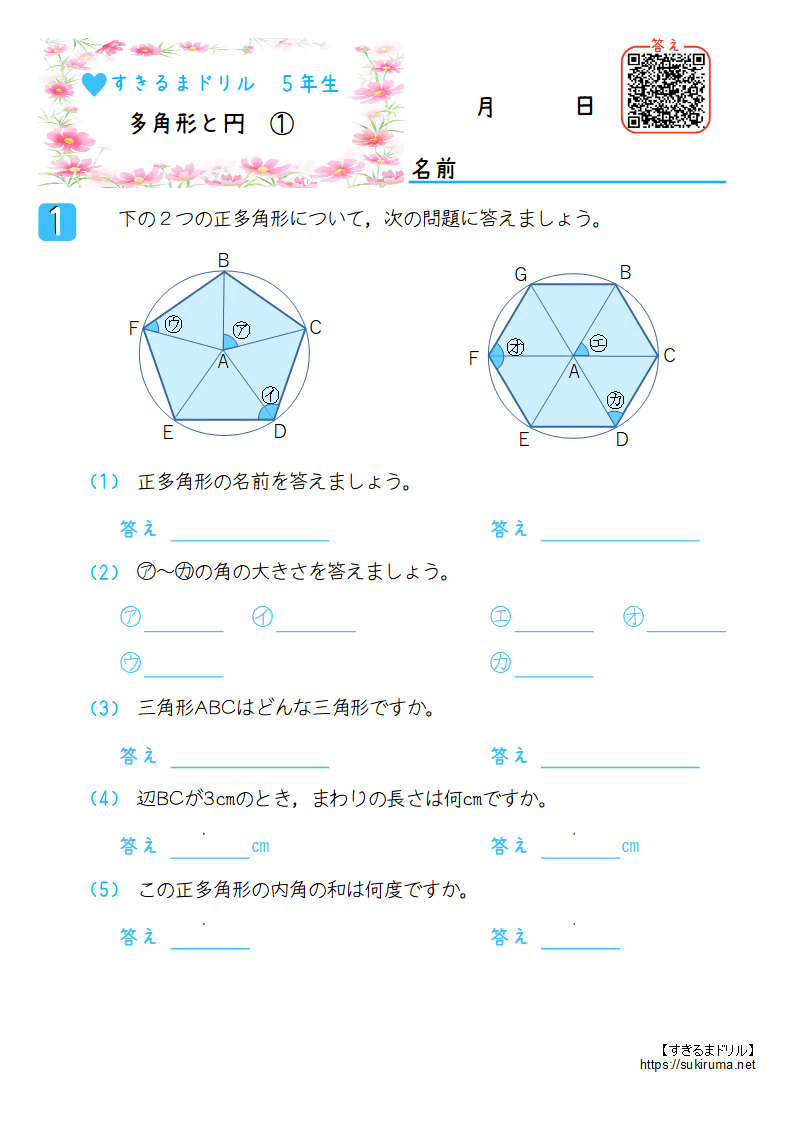



すきるまドリル 小学5年生 算数 多角形と円 無料学習プリント すきるまドリル 無料学習プリント



一辺の長さが3cmの正八角形はどうやってかけますか 教えてください お願い Yahoo 知恵袋



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



八角形のお盆



円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ




正八角形の対角線の本数 おときち副塾長 電脳空間学習塾かもん Youtube



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



正八角形を作りたく一辺の長さを計算したいです 日曜大工を Yahoo 知恵袋



図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦



1
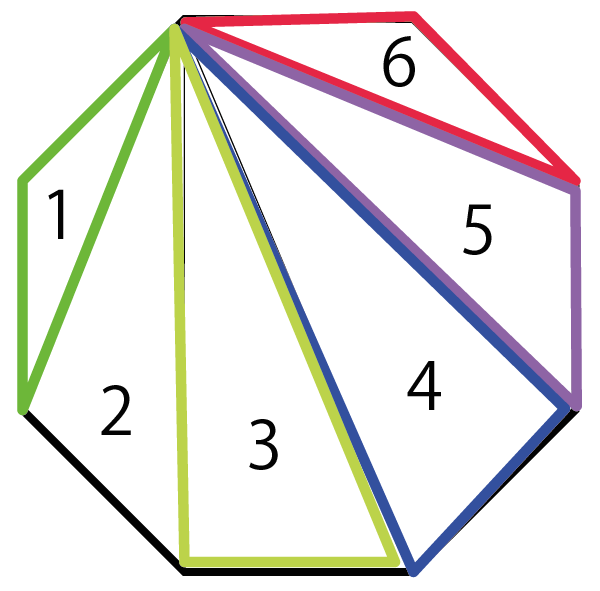



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




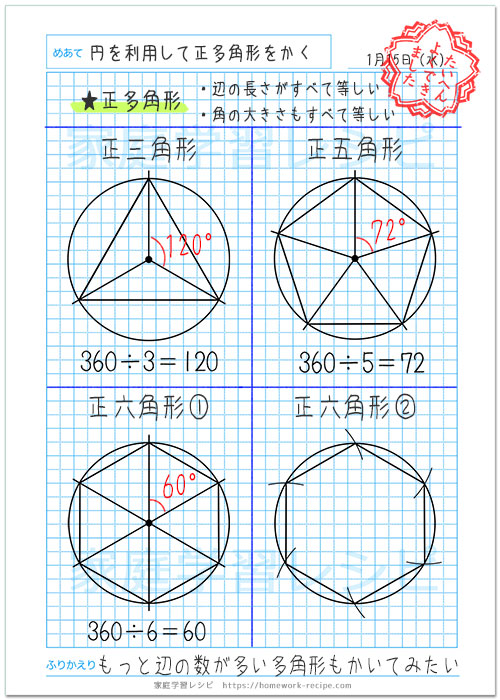
今日は 円を使って正多角形をかく自主学習をしてみましょう 正多角形は 多角形の中で次のような条件を満たすものです すべての辺が同じ長さ すべての角が同じ長さ 正三角形や正方形も 学習ノート 学習 正多角形




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月



一辺の長さが1cmの正八角形の面積をわかりやすく詳しく教えて下さい よろ Yahoo 知恵袋




半径2の円に内接する正五角形の一辺の長さ の求め方 Youtube



正多角形の描き方



1



Happylilac Net Seitakakkei Ans Pdf



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度



5年算数 円と正多角形 2 わかる教え方のポイント
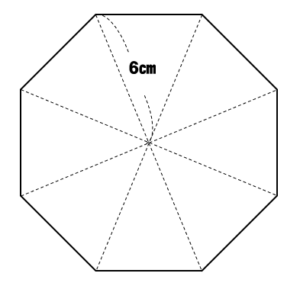



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ
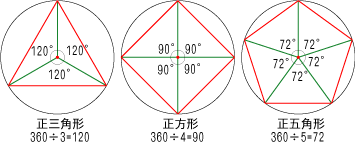



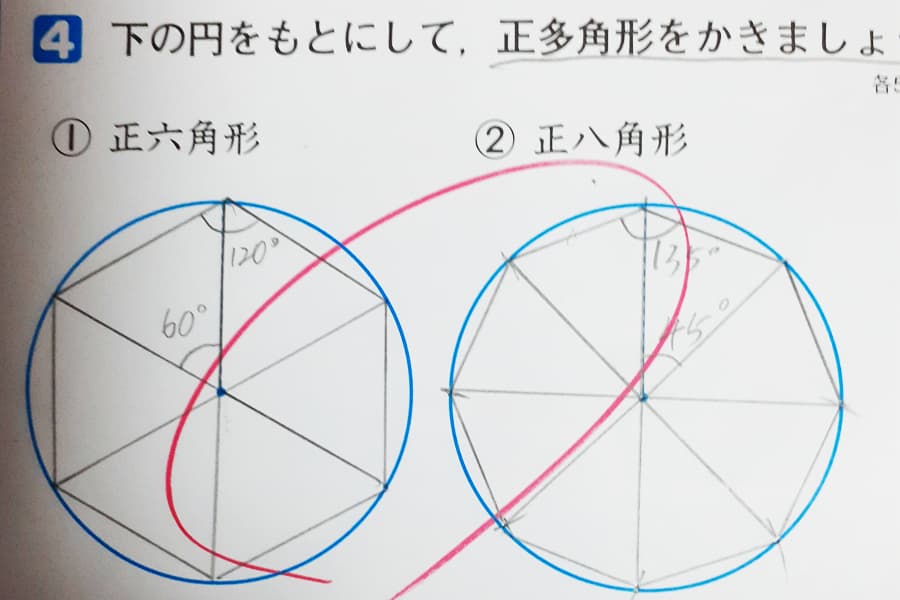
正多角形の作図 5年生 算数の広場




八角形の周囲と面積を計算する方法
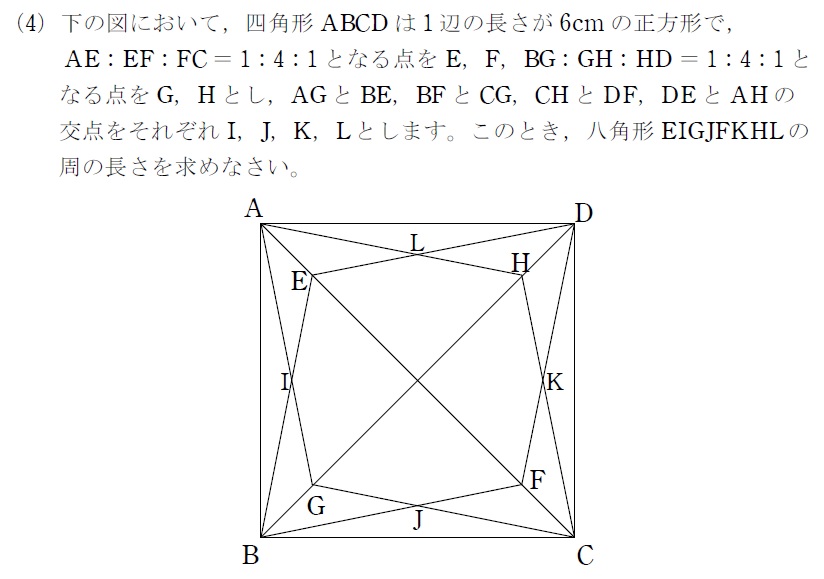



家庭教師サボ 正八角形ではないものの図形全体が対称的なので この八角形の辺の長さ はすべて等しい Oad Oehから内部にある1辺4cmの正方形を見つける 赤線が1cm Adl Helでlq 2 5cm Leqで三平方 El 2 26 5cm これを8倍




八角形の周囲と面積を計算する方法




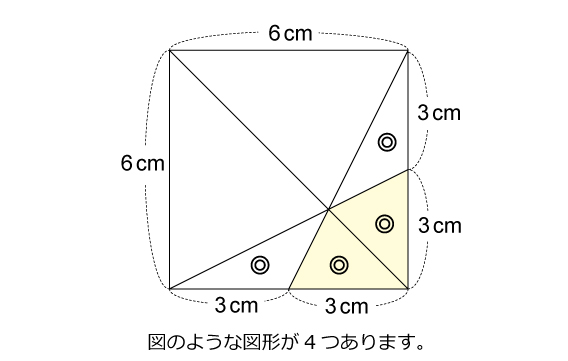
図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦




数a 場合の数 8角形 一辺を共有する三角形 Youtube




高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット
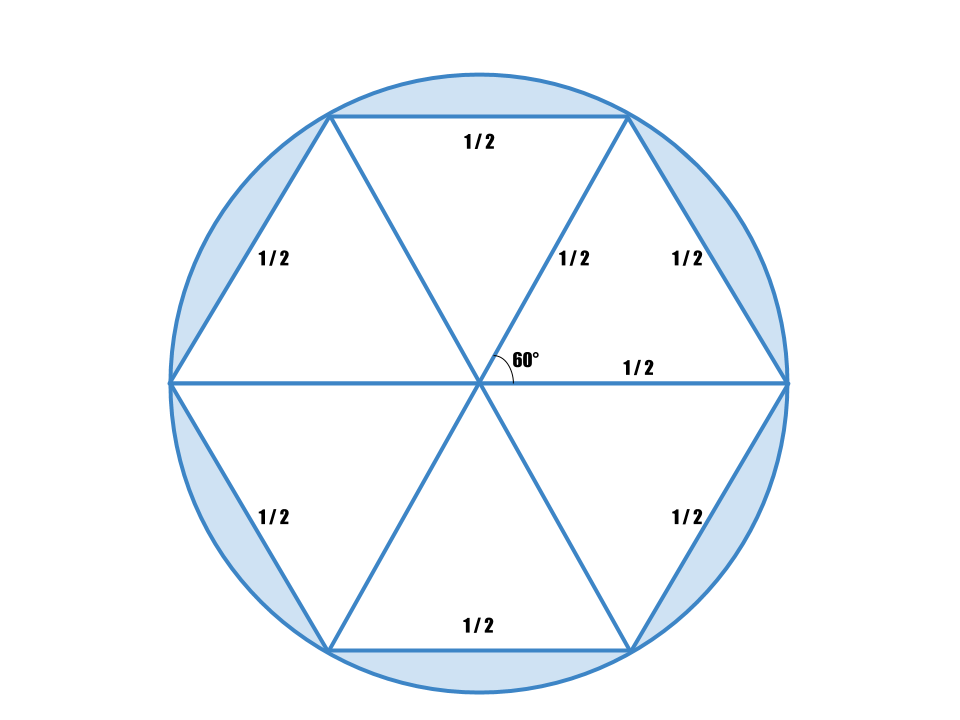



東大入試解説 円周率が3 05よりも大きいことを証明せよ




5年算数 円と正多角形 1 わかる教え方



一辺の長さが1の正八角形の面積の求め方を教えてください 答えは2 Yahoo 知恵袋




高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット




八角形の周囲と面積を計算する方法



八角形の一辺の長さを求める公式を教えてください 例えば1700の正方形で Yahoo 知恵袋



正多角形の公式 面積 周囲の長さ 頂点の角度 対角線の本数 辺の長さ 数学 エクセルマニア
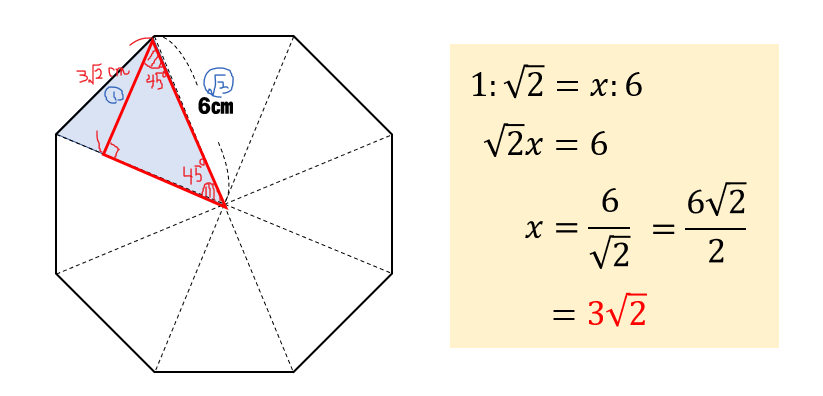



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ
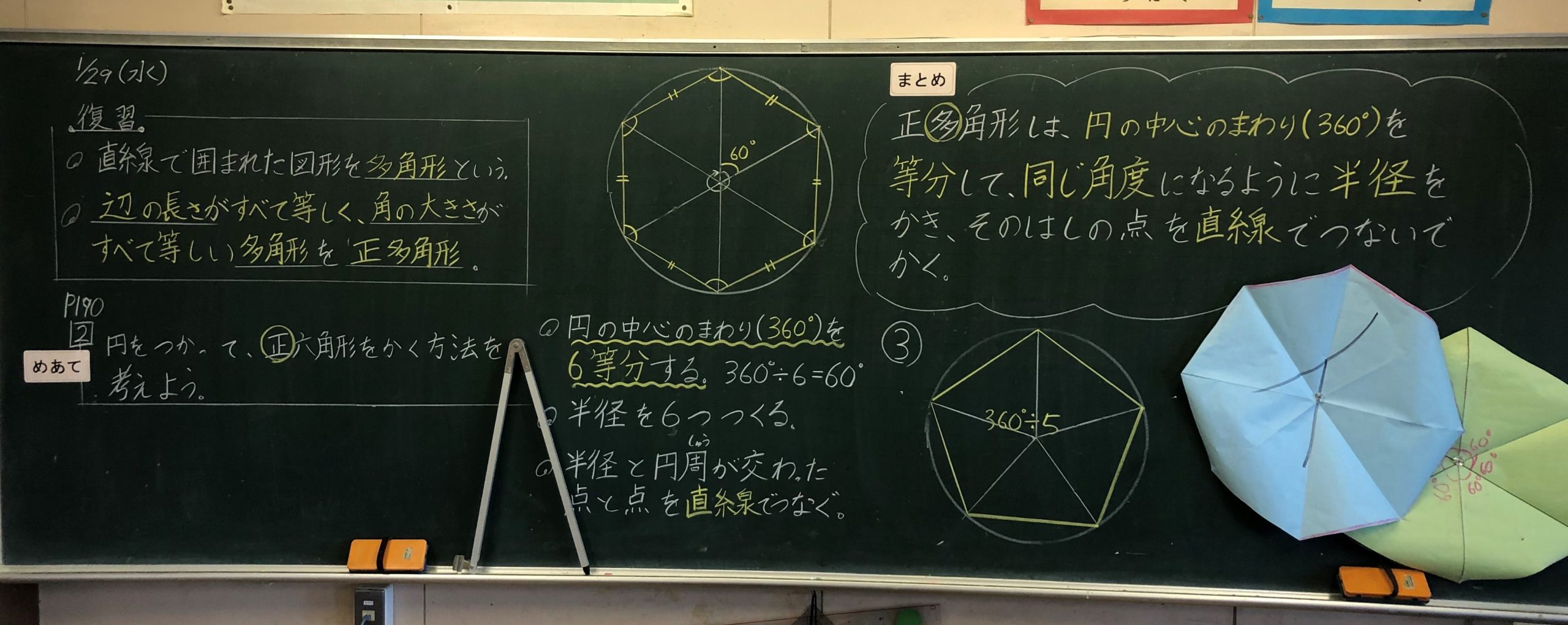



5年生算数 円と正多角形 黒板log




高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット



1



円周率は 3 00 以上であることを証明せよ 受験算数入門
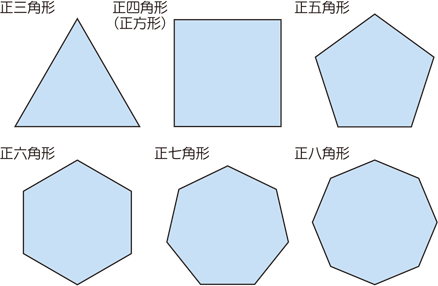



正多角形 算数用語集




正多角形の面積 倭算数理研究所
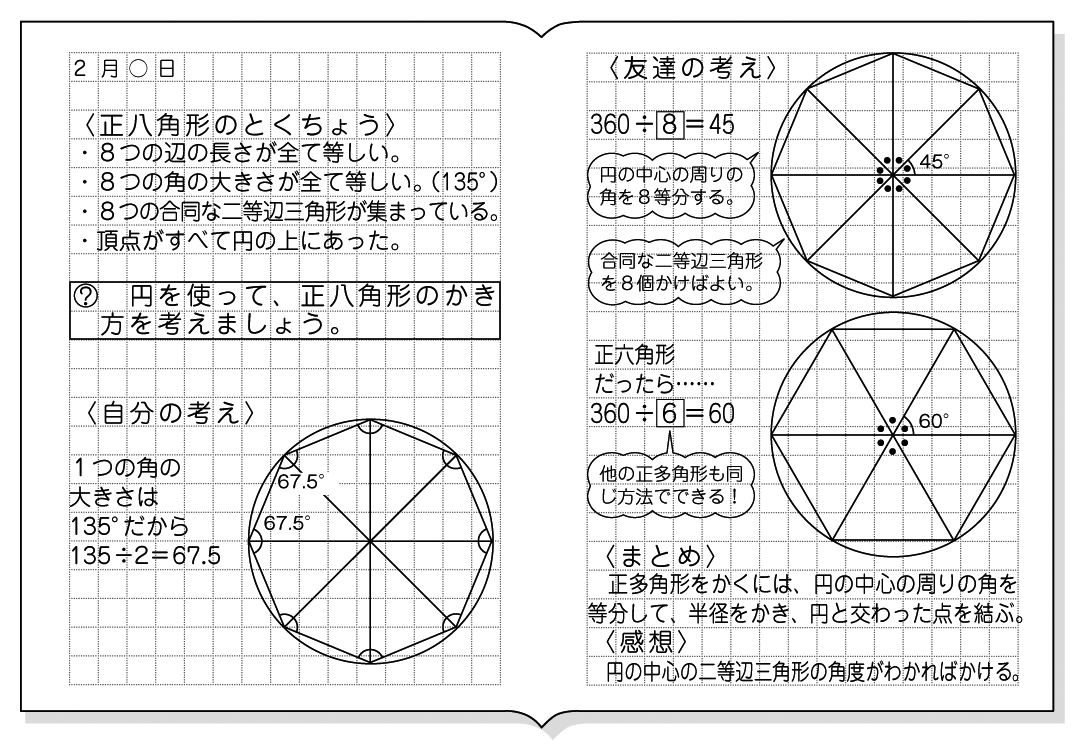



小5算数 正多角形と円 指導アイデア みんなの教育技術



2b 第4問 16年 追試 センター試験数学解説 おおぞらラボ




八角形の周囲と面積を計算する方法


